Parallel Resistance Chart |
|
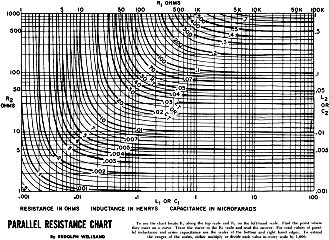
If you have ever placed a fixed resistor in parallel with a potentiometer to reduce the total resistance, then you are familiar with how you also convert a linear relationship of the wiper movement with resistance to one that is nonlinear. That is because the equation changes from Rtotal = Rx:potentiometer (where x is the potentiometer position) to Rtotal = (Rx:potentiometer * Rparallel) / (Rx:potentiometer + Rparallel). The graph of it looks like one of the curves in this chart. Since the total parallel resistance is always smaller than the lowest value of the two resistances, the greater the ratio of the two is, the more dominant the smaller resistance value becomes. That means as the potentiometer wiper approaches the minimum resistance end of its travel, the parallel resistor attached across it has virtually no effect. Since parallel-connected inductors and series-connected capacitors scale in the same manner as parallel-connected resistors, this chart is useful for those circuits as well. Series-connected resistors and inductors, and parallel-connected capacitors are simply the sums of their individual values. Consequently, if you connect a fixed resistor in series with a potentiometer, the total resistance at any position of the potentiometer wiper will be the linear sum of the fixed resistor and the potentiometer resistance. Got that? * Theoretically, x is a value from 0 to 1 that represents the relative position of the potentiometer wiper contact. Parallel Resistance Chart To use the chart locate R1 along the top scale and R2 on the left-hand scale. Find the point where they meet on a curve. Trace the curve to the RT scale and read the answer. For total values of parallel inductance and series capacitance use the scales at the bottom and right hand edges. To extend the ranges of the scales, either multiply or divide each value in every scale by 1,000.
Posted June 9, 2022 |
|